TP Nº4
1) Para las compuertas: AND, OR y XOR. De 2, 3 y 4 entradas, escribir: simbolo, funcion, tabla de verdad.
2) Definir: bit y byte
3) Inversor: 2, 3 y 4 entradas,poner simbolo, funcion, tabla de verdad
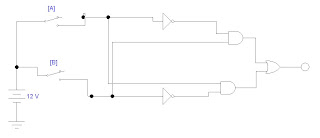
4) Para el siguiente circuito indicar el valor de la variable para cada uno de los puntos indicados:
5) Para las compuertas: NAND, NOR, XNOR.simbolo y tabla de verdad
6) Para los siguientes circuitos dar la funcion en la tabla de verdad
7) Para las siguientes funciones dar el circuito y la tabla de verdad
1- OR
La puerta lógica O, más conocida por su nombre en inglés OR (A+B), realiza la operación de suma lógica.
Simbolo:+
A | B | C | F |
0 | 0 | 0 | 0 |
0 | 0 | 1 | 1 |
0 | 1 | 0 | 1 |
0 | 1 | 1 | 1 |
1 | 0 | 0 | 1 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 1 |
1 | 1 | 1 | 1 |
A | B | C | D | F |
0 | 0 | 0 | 0 | 0 |
0 | 0 | 0 | 1 | 1 |
0 | 0 | 1 | 0 | 1 |
0 | 0 | 1 | 1 | 1 |
0 | 1 | 0 | 0 | 1 |
0 | 1 | 0 | 1 | 1 |
0 | 1 | 1 | 0 | 1 |
0 | 1 | 1 | 1 | 1 |
1 | 0 | 0 | 0 | 1 |
1 | 0 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 1 |
1 | 0 | 1 | 1 | 1 |
1 | 1 | 0 | 0 | 1 |
1 | 1 | 0 | 1 | 1 |
1 | 1 | 1 | 0 | 1 |
1 | 1 | 1 | 1 | 1 |
A | B | F |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
AND
La puerta lógica Y,
más conocida por su nombre en
inglés AND (A*B), realiza la función booleana de producto lógico. Su símbolo es un punto (·), aunque se suele omitir
Simbolo: · o *
A | B | C | D | F |
0 | 0 | 0 | 0 | 0 |
0 | 0 | 0 | 1 | 0 |
0 | 0 | 1 | 0 | 0 |
0 | 0 | 1 | 1 | 0 |
0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 1 | 0 |
0 | 1 | 1 | 0 | 0 |
0 | 1 | 1 | 1 | 0 |
1 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 1 | 0 |
1 | 0 | 1 | 0 | 0 |
1 | 0 | 1 | 1 | 0 |
1 | 1 | 0 | 0 | 0 |
1 | 1 | 0 | 1 | 0 |
1 | 1 | 1 | 0 | 0 |
1 | 1 | 1 | 1 | 1 |
A | B | C | F |
0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 |
0 | 1 | 0 | 0 |
0 | 1 | 1 | 0 |
1 | 0 | 0 | 0 |
1 | 0 | 1 | 0 |
1 | 1 | 0 | 0 |
1 | 1 | 1 | 1 |
A | B | F |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
XOR
La puerta lógica OR-
exclusiva, más conocida por su nombre en inglés XOR, realiza la función booleana A'B XOR AB'. Su símbolo es el más (+) inscrito en un círculo
A | B | F |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
A | B | C | D | F |
0 | 0 | 0 | 0 | 0 |
0 | 0 | 0 | 1 | 1 |
0 | 0 | 1 | 0 | 1 |
0 | 0 | 1 | 1 | 0 |
0 | 1 | 0 | 0 | 1 |
0 | 1 | 0 | 1 | 0 |
0 | 1 | 1 | 0 | 0 |
0 | 1 | 1 | 1 | 1 |
1 | 0 | 0 | 0 | 1 |
1 | 0 | 0 | 1 | 0 |
1 | 0 | 1 | 0 | 0 |
1 | 0 | 1 | 1 | 1 |
1 | 1 | 0 | 0 | 0 |
1 | 1 | 0 | 1 | 1 |
1 | 1 | 1 | 0 | 1 |
1 | 1 | 1 | 1 | 0 |
A | B | C | F |
0 | 0 | 0 | 0 |
0 | 0 | 1 | 1 |
0 | 1 | 0 | 1 |
0 | 1 | 1 | 0 |
1 | 0 | 0 | 1 |
1 | 0 | 1 | 0 |
1 | 1 | 0 | 0 |
1 | 1 | 1 | 1 |
2-
Bit es el acrónimo de Binary digit. (dígito binario). Un bit es un dígito del sistema de numeración binario.
Byte es una palabra inglesa que si bien
ceptado como equivalente a octeto (es decir a ocho bits), para fines correctos, un byte debe ser considerado como una secuencia de bits contiguos, cuyo tamaño depende del código de información o código de caracteres en que sea definid
o.
3-
A | Ā |
0 | 1 |
1 | 0 |
4-
5-
NAND
La puerta lógica NO-Y, más conocida por su nombre en inglés NAND, realiza la operación de producto lógico negado.
A | B | F |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Simbolo:
NOR
La puerta lógica NO-O, más conocida por su nombre en inglés NOR, realiza la operación de suma lógica negada
Simbolo:
XNOR
La puerta lógica equivalencia, realiza l
a función booleana AB+~A~B. Su s
ímbolo es un punto (·) inscrito en un círculo
Simbolo:
6)-
10-Construir un circuito capas de sumar 2 numeros de un bit. Debe dar la suma (S) y el acarreo (CY)
Binario.
0+0=0
0+1=1
1+0=1
1+1=10
Acarreo(carey) 1 + 1 =1 0 Suma
A | B | S | CY |
0 | 0 | 0 | 0 |
1 | 0 | 1 | 0 |
0 | 1 | 1 | 0 |
1 | 1 | 0 | 1 |
S= A+B
Cy= A .B
A | Ci | B | S | Cs |
0 | 0 | 0 | 0 | 0 |
0 | 0 | 1 | 1 | 0 |
0 | 1 | 0 | 1 | 0 |
0 | 1 | 1 | 0 | 1 |
1 | 0 | 0 | 1 | 0 |
1 | 0 | 1 | 0 | 1 |
1 | 1 | 0 | 0 | 1 |
1 | 1 | 1 | 1 | 1 |
S=A B C
Cyo =ABC + ABC + ABC + ABC
12-Mediante bloques de circuitos
semi sumadores y sumadores construir un circuito capaz de sumar dos numeros de 4 bits

13-Construir un circuito capas de restar 2 numeros binarios de 4 bits usando la tecnica del complmente A2. en todos los casos elminoendo sera mayor del sustraendo.

14-Construir un circuito capaz de restar 2 numeros binarios de 4 bit usando la tecnica del complemento a 2. En todos los casos el minuendo sera mayor que el sustraendo

15- Construir un circuito capaz de sumar o restar 2 numeros de 4 bit de acuerdo a la pocision de una llave. Nota: en el caso de la resta el minuendo siempre sera mayor que el sustraendo.